Note
Click here to download the full example code
Usage¶
The usage example assumes the package is imported as:
import local2global as l2g
For consistent results, fix the seed for the random number generator:
l2g.utils.seed(42)
Generate synthetic test data and patches¶
The goal for the local2global algorithm is to transform a set of separate patch embeddings into a global node embedding.
The assumptions are that the patch embeddings perturbed parts of a global node embedding where the perturbations consist
of scaling, rotation, reflection, translation and random noise. To work, the patches need to overlap such that the
patch graph forms a single connected component where we consider a pair of patches to be connected if they share
at least dim + 1 nodes (dim is the embedding dimension).
For illustration and testing purposes, the package contains code to generate artificial test data
(see local2global.example).
This is not imported by default and to make it available use:
import local2global.example as ex
Also import matplotlib to visualise the results:
import matplotlib.pyplot as plt
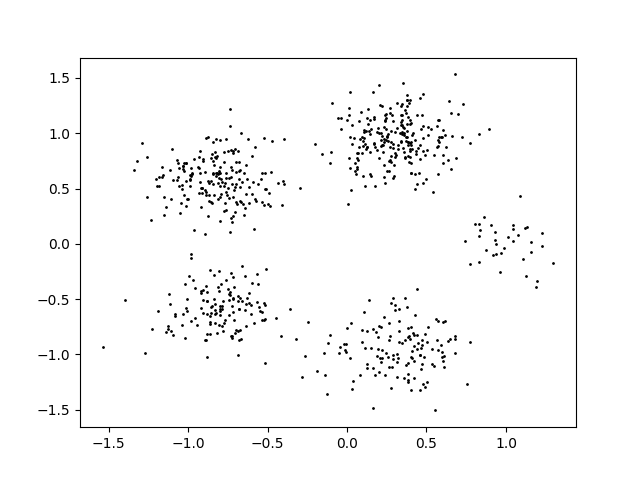
First generate a ground-truth embedding using generate_data(). In this example,
we generate data with 5 clusters, where each cluster has a maximum size of 300 points, points within each cluster are
normally distributed with a standard deviation of 0.2, and cluster centers are uniformly spaced on the unit circle.
points = ex.generate_data(n_clusters=5, max_size=300, std=0.2)
Visualise the data:
plt.scatter(points[:, 0], points[:, 1], s=1, c='k')
plt.show()
Next, we split the test data into 10 overlapping patches using Voronoi_patches().
patches = ex.Voronoi_patches(points=points, sample_size=10, eps=1.5, kmeans=True)
In this case we first identify the patch centers using k-means clustering and assign points to the patch with the
nearest center and any other patch whose center is within 1.5 times the distance to the nearest center. Patches may be
expanded further to satisfy some connectivity constraints on the patch graph
(see Voronoi_patches())
Local2global algorithm¶
Set up alignment problem¶
The main interface to the local2global algorithm is provided by AlignmentProblem which
weights each patch edge equally and WeightedAlignmentProblem which weights patch
edges by the size of the patch overlap and can be more robust when patch overlaps are heterogeneous. Both classes
implement the same interface and expect a list of Patch objects (such as generated by
Voronoi_patches()) as the main input and accept some other options to control the
behaviour. Here we use the default options:
problem = l2g.AlignmentProblem(patches)
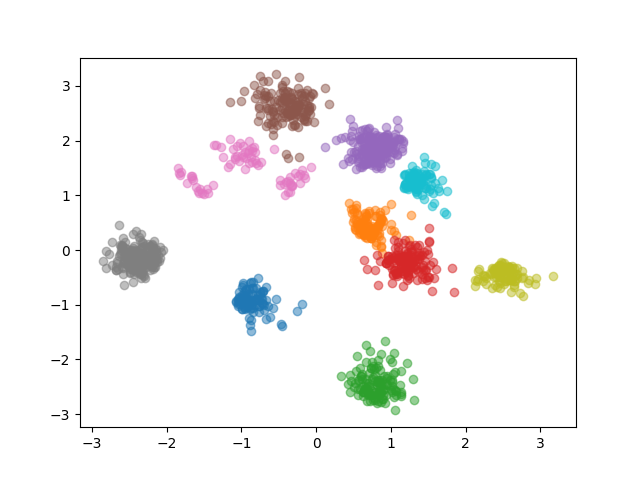
Perturb the patch embeddings¶
For testing we add some random rotations/reflections, shifts and normally distributed noise to the patch embeddings:
true_rotations = ex.rand_rotate_patches(problem)
true_shifts = ex.rand_shift_patches(problem, shift_scale=1)
ex.add_noise(problem, 0.01)
Visualise the results:
for p in problem.patches:
plt.scatter(p.coordinates[:, 0], p.coordinates[:, 1], alpha=.5)
plt.show()
For comparison we also set up a weighted problem with the same noise:
weighted_problem = l2g.WeightedAlignmentProblem(problem.patches)
Recover global embedding¶
Use
recovered_points = problem.get_aligned_embedding()
recovered_points_weighted = weighted_problem.get_aligned_embedding()
to run the local2global algorithm and reconstruct the global embedding. The results are cached and subsequent calls to
get_aligned_embedding() return the cached result without rerunning the
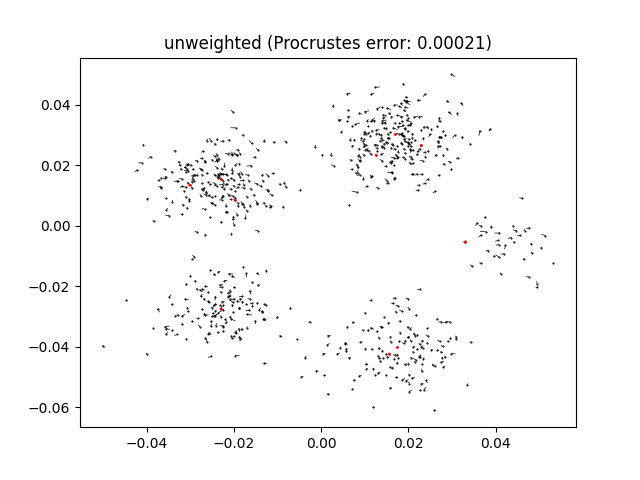
algorithm unless run with realign=True. We can visualise the reconstruction error using
error = ex.plot_reconstruction(points, problem)
plt.title(f"unweighted (Procrustes error: {error:.3g})")
plt.show()
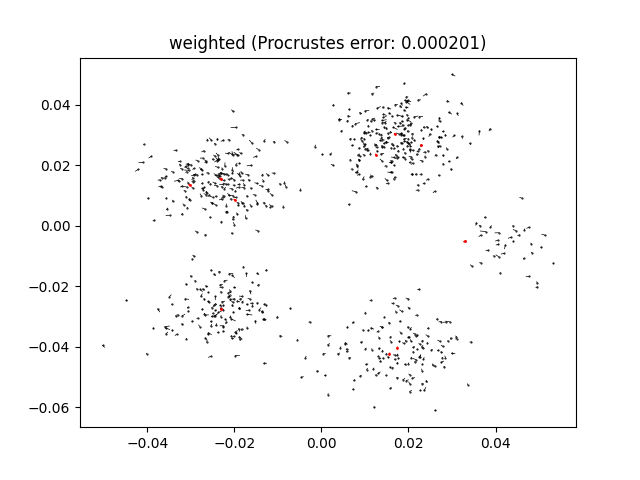
and
error_weighted = ex.plot_reconstruction(points, weighted_problem)
plt.title(f"weighted (Procrustes error: {error_weighted:.3g})")
plt.show()
Total running time of the script: ( 0 minutes 22.092 seconds)